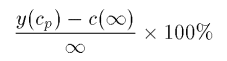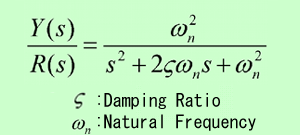
Interactive Control Systems Tools
Control systems analysis
Analysis of a 2-nd order systems (time domain)

Step response of a second order systems

The transfer function of a 2-nd order system is generally represented by the following transfer function:

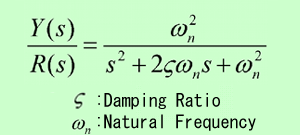
The dynamic behavior of the second-order system can then be described in terms of two parameters: the damping ratio and the natural frequency.

If the dumping ratio is between 0 and 1, the system poles are complex conjugates and lie in the left-half s plane. The system is then called underdamped, and the transient response is oscillatory. If the damping ratio is equal to 1 the system is called critically damped, and when the damping ratio is larger than 1 we have overdamped system. The transient response of critically damped and overdamped systems do not oscillate. If the damping ratio is 0, the transient response does not die out.

Depending on the values of the damping ratio the equations describing the system response have the following forms:

(1) Underdamped system

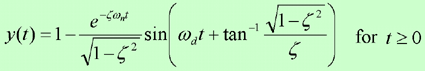
(2) Critically damped system

(3) Overdamped system

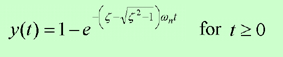
(4) Undamped system

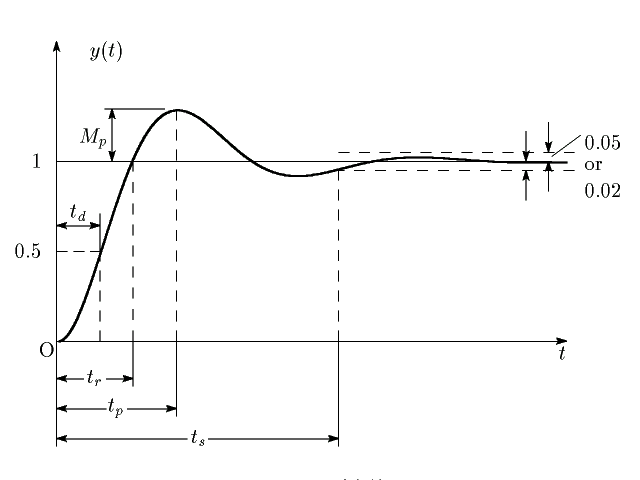
Definitions of transient-response specifications

In many practical cases, the desired performance characteristics of control systems are specified in terms of time domain quantities. Systems with energy storage cannot respond instantaneously and will exhibit transient responses whenever they are subjected to inputs or disturbances.

Frequently, the performance characteristics of a control system are specified in terms of the transient response to a unit-step input since it is easy to generate and is sufficiently drastic. (If the response to a step input is known, it is mathematically possible to compute the response to any input).

The transient response of a system to a unit-step input depends on the initial conditions, but for convenience in comparing the transient-responses of various systems, it is common practice to use zero initial conditions. In specifying the transient-response characteristics of a control system to a unit-step input, it is common to specify the following:

1. Delay time (td)

The delay time is the time required for the response to reach half the final value the very first time.

2. Rise time (tr)

The rise time is the time required for the response to rise from 10% to 90%, 5% to 95%, or 0% to 100% of its final value. For underdamped second-order systems, the 0% to 100% rise time is normally used. For overdamped systems, the 10% to 90% rise time is commonly used.

3. Peak time (tp)

The peak time is the time required for the response to reach the first peak of the overshoot.

4. Maximum (percent) overshoot (Mp)

The maximum overshoot is the maximum peak value of the response curve measured from unity. If the final steady-state value of the response differs from unity, then it is common to use the maximum percent overshoot. It is defined by

5. Settling time (ts)

The settling time is the time required for the response curve to reach and stay within a range about the final value of size specified by absolute percentage of the final value (usually 2% or 5%). The settling time is related to the largest time constant of the control system.

References:

K. Ogata, Modern control engineering, Third edition, Prentice-Hall, Upper-Saddle River, NJ 07458, 1997.