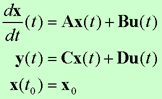
Interactive Control Systems Tools
Control systems design
State Feedback

State Feedback

Consider a control system

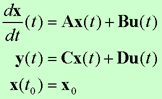
where all system variables are measurable and are available for feedback.

Choose a control signal

This means that the control signal is determined by an instantaneous state. Such a scheme is called state feedback. The matrix F is called the state feedback gain matrix. In the following analysis it is assumed that u(t) is unconstrained.

The figure shows the system defined by the above equations.

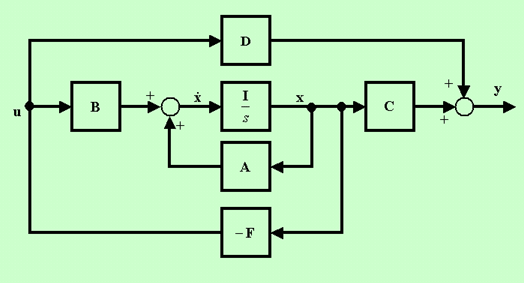
The overall system is described by

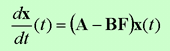
The stability and transient response are determined by the eigenvalues of matrix A-BF. If the matrix F is chosen properly, the matrix A-BF can be made asymptotically stable matrix, and for all nonzero initial conditions it is possible to make the states approach 0 as the time approaches infinity. The eigenvalues of matrix A-BF are called the regulator poles. If these regulator poles are placed in the left-half s plane, then the states approach 0 as t approaches infinity. The problem of placing the closed-loop poles at desired location is called pole placement problem.